第78回 知の拠点セミナー
第78回 知の拠点セミナー
講演1 「現代ものづくりの背後にある巨大な連立一次方程式に挑む」 / 講演2 「ガラス原板ネガ写真にみる幕末・明治初期の日本」
| 日時 | 平成30年9月21日(金) 18時00分~20時00分(※17時30分から受付開始) |
|---|---|
| 場所 | 東京大学地震研究所1号館2階セミナー室 ※6月から開催場所が変わりました (東京都文京区弥生1-1-1:アクセスマップ)南北線東大前駅徒歩約5分 |
| プログラム |
- 第78回セミナー 申込ページ 9月19日(水) 16時まで (定員に達し次第締め切ります)
- お問い合わせ:jurc-seminar[at]eri.u-tokyo.ac.jp まで
講演1:「現代ものづくりの背後にある巨大な連立一次方程式に挑む」
岩下 武史(北海道大学情報基盤センター 副センター長/教授)

現在、様々な「ものづくり」においてコンピュータによるシミュレーションが欠かせないものとなっている。このようなコンピュータを活用した工学は「CAE: Computer Aided Engineering」と呼ばれ、その中では構造力学、流体力学、電磁場、音響、プラズマといった様々な物理現象が扱われる。CAE分野のシミュレーションでは、一般に有限要素法や境界要素法などの離散化解法が用いられる。こうした離散化解法では、解析対象である物体や空間を格子あるいはメッシュにより細分化し、格子点や辺上におかれた未知変数、例えば、圧力や磁場といった物理量の値を算出する。この際、多くの離散化解法では、連立一次方程式を解くことによりこれらの値を定める。
連立一次方程式の求解に必要な計算量は一般に多大であり、CAE分野のシミュレーションでは、全体の計算時間の大部分が方程式の求解に費やされることも珍しくない。そのため、従来から高速な連立一次方程式の求解法が求められ、活発な研究がなされてきた。しかしながら、近年のものづくり分野では、性能(省電力性能等)や設計期間に関する要求が増大しており、これらの要求に応える高精度/高速解析を実現するために、超大規模な連立一次方程式をより高速に解く方法が求められている。
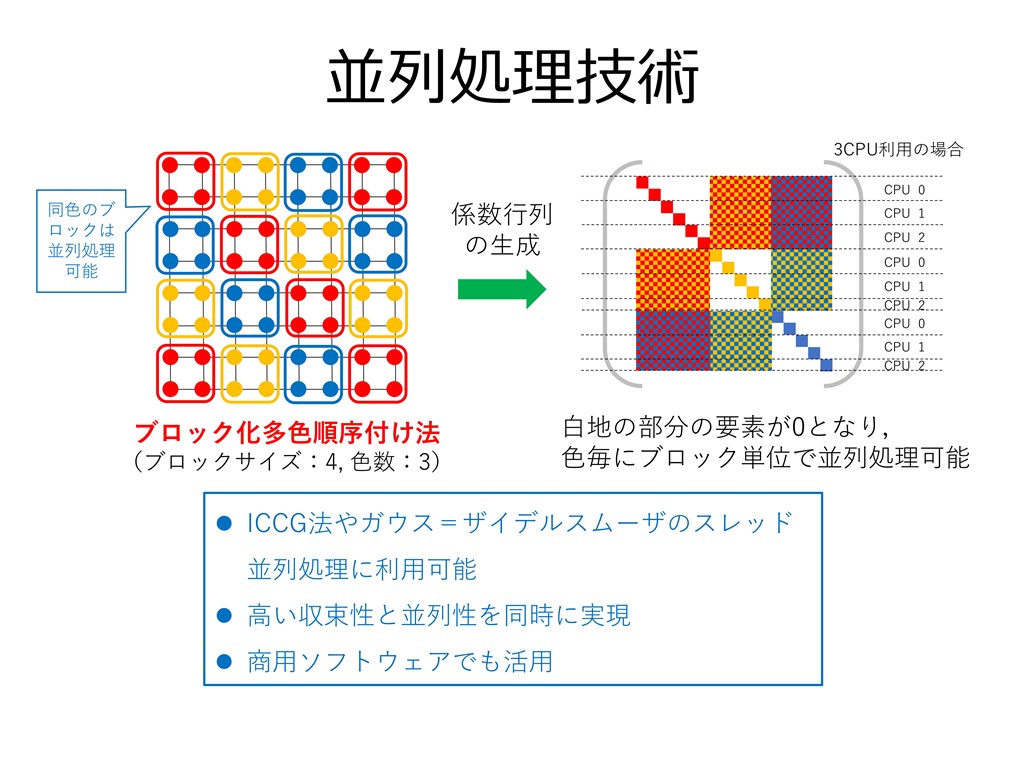
本講演では、まずコンピュータシミュレーションにおいて、どのような連立一次方程式がどのように解かれるのか、その基本的解法について概説する。次に、CAE分野においてよく用いられる求解法である「反復法」に焦点を当て、その高速化技術について数理的側面、計算機科学的側面の両面から講演者の研究成果を交えて紹介する。最後に、ポストムーア時代と言われる今後の計算機の将来像を踏まえた技術展望について述べる。
.jpg)
講演2:「ガラス原板ネガ写真にみる幕末・明治初期の日本」
保谷 徹(東京大学史料編纂所 所長/教授)

東京大学史料編纂所は、国内外に所在する日本史の史料を調査・研究しています。この史料には、いわゆるテキストのみならず、さまざまな画像史料も含まれます。今回は、附属画像史料解析センター古写真研究プロジェクトの研究を取り上げ、遠くオーストリアで「発見」された2つの湿板写真ガラス原板ネガ・コレクションを紹介します。1869年に来日した写真家ブルガーとその弟子モーザーのコレクションには、撮影した本人が思いもよらなかった高精細な画像情報が写し込まれていました。約260枚のガラス原板ネガから、幕末・明治初期の日本の姿を読み解きます。

日本橋(カンマーホフ博物館寄託モーザーコレクション)
![]()
赤坂門内の旧大名屋敷(カンマーホフ博物館寄託モーザーコレクション)





